삼각기둥 부피 공식 상세정리

삼각뿔의 부피를 어떻게 구하는지 알아보겠습니다

같이 알아두면 좋은 정보

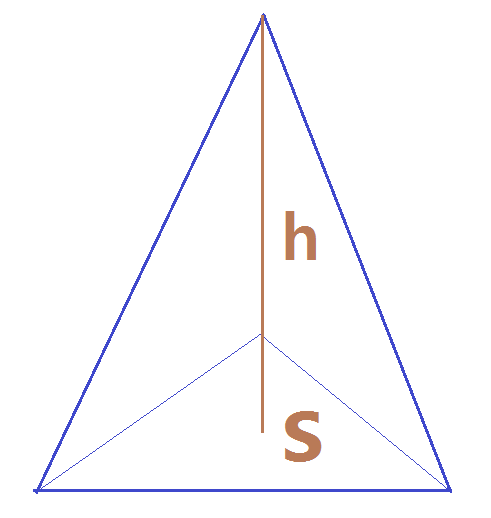
밑면적이 S 이고높이가h 인 저런 삼각뿔이 있습니다

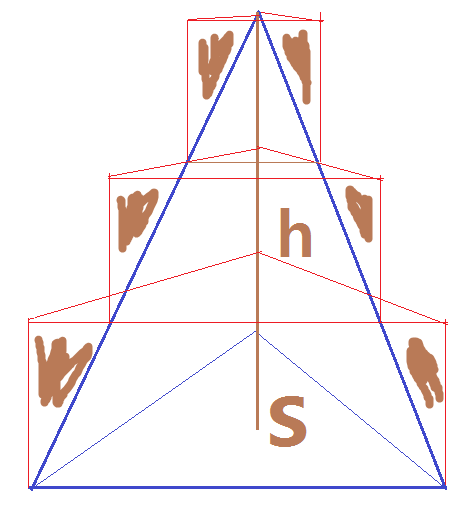
똑 같은 높이외접하는 삼각기둥 3 개로삼각뿔을 둘러샀습니다각각의 삼각기둥의 높이는 모두

입니다

3 개의 삼각기둥은 모두 닮은 꼴입니다

맨 위의 삼각기둥 밑면적 한 변 길이가 맨 아래 삼각기둥 밑면적 한 변 길이의

이니까면적닮음은 길이닮음의 제곱이라는 중학교 수학에 의해맨 위의 삼각기둥밑 면적은

같이 알아두면 좋은 정보

그 다음 가운데 삼각기둥은 밑면적 한 변 길이가

맨 아래 삼각기둥 밑면적 한 변 길이의

이니까면적닮음은 길이닮음의 제곱이라는 중학교 수학에 의해가운데 삼각기둥밑 면적은

맨 아래 삼각기둥 밑면적은 자기 자신이니까 그냥

같이 알아두면 좋은 정보

같은 높이로 분할했으니까각각의 삼각기둥 높이는 모두가

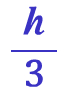
입니다그리고 각각의 높이는 방금 이야기 했습니다그런데

3 개의 삼각기둥 부피를 합쳐도삼각뿔 부피가 되지 않습니다색칠한 부분처럼 튀어나온 부분의 오차가 있기 때문입니다무수히 수많은저 오차를 없애려면무수히 수많은 무한개의 삼각기둥의 부피를 합쳐야 합니다

일단n 개의 삼각기둥으로 생각하겠습니다

그림을 그리기 어려우니저것을 n 개의 삼각기둥이라고 생각해 주시기 바랍니다맨 위부터 ~~ 맨 밑까지각각의 삼각기둥의 부피를 합치겠습니다(앞에서 3 개로 했을 경우를 참고로 하면 이해가 갈 겁니다)이번에는 3 개가 아니라 n 개 입니다

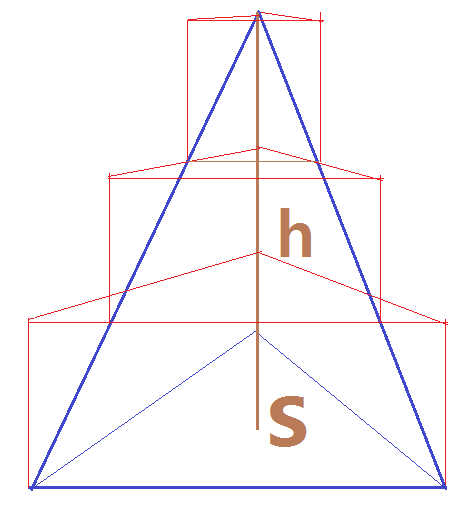
그림을 그리기 어려우니n 개의 삼각기둥이라 생각하고각각의 부피를 합치겠습니다(밑면적×높이 = 부피 ...... 이것을 맨 위부터 계속 합칩니다)

저것이 n 개의 원기둥의 부피의 합인데

색칠한 부분의 오차를 없애고완전하게 삼각뿔의 부피를 구하려면3 개로 해서는 미친 짓이고n 개로 해도 어림도 없고무수히 수많은 삼각기둥으로 외접시켜야 한다고 했습니다그래서 n 에다 무한대를 대입해야 합니다

삼각뿔 부피 구하는 공식이 나옵니다사각뿔 또한 부피공식이 같은 것은이런 이유라고 생각하면 되겠습니다 ~~

원뿔, 삼각뿔, 사각뿔..등.. 모든 각뿔의 넓이 공식은 1/3을 기억하면 된다. 원기둥이나 삼각기둥 등 밑면의 단면적과 윗면의 단면적이 같은 입체도형의 부피는 밑면의 넓이 ×높이가 된다. 여기서 높이에 따라 밑면의 넓이가 일정하게 줄어들어 뿔(점)의 형태가 되는 도형의 넓이는 원래 기둥의 넓이의 1/3이 된다.

삼각뿔, 사각뿔도 마찬가지다.

원리 생각해보기

적분을 통해 증명을 할 수도 있지만, 여기서는 기하를 통해 원리를 파악해보자.

위 그림은 직육면체를 사각뿔과 나머지 입체도형으로 분해한 것이다. 4개의 동일한 모양의 사각뿔이 나오므로 총 5개의 사각뿔이 나온다.5개의 사각뿔의 합이 총 입체도형인 직육면체의 부피이므로 등식을 세워서 계산해보자. 여기서 전제 되어야 할 것은 모든 각뿔들은 밑변의 넓이와 높이가 동일한 기둥의 부피와 일관된 비례 관계가 성립한다는 전제를 세워야 한다. 우리는 이미 비례 관계가 성립되는 것을 알기 때문에 이 공식을 이런 식으로 구할 수 있다.